2022年省考行测判断推理难点之图形推理--元素的运换算
图形推理是每年省考必考的题目, 而关于素的考点在近几年都有出现,元素的运换算在图形推理当中是较难的一类题目,一步一步的试错,再运算,再进一步的替换都会浪费大量的时间,因此大多数考生均选择放弃 ,但是如果我们能够突破这一难点,是可以获得一定优势的。
元素的运换算有两种表现形式,一种是涉及等差数列的运换算,一种是涉及等比数列的,华图教育对涉及等差数列 的元素运换算的题目进行讲解。
元素运换算题型识别:
①图形一般由两种元素组成;
②单种元素没有明显的数量变化规律,两种元素间也没有加减乘除的规律。
解题步骤:
① 先运算
② 后替换
解题方法(任意连续的三个图):
加减法(等差数列):第一图+第三图 =2*第二图
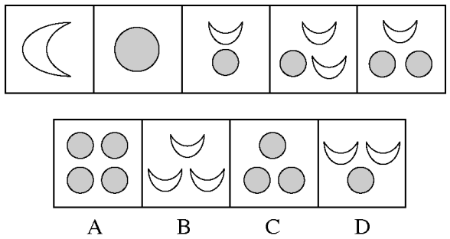
【例1】 从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
【华图解析】 C
第一步,观察特征。
组成元素不同,优先考虑数量类或属性类。图形均由小元素组成,考虑数量类的元素。
第二步,两段式,第一段找规律,第二段应用规律。
思维1: 首先观察元素的种类或者个数,发现没有规律,再观察元素之间的加减乘除关系,仍然 无 规律 。 因此,考虑元素的运换算 :① 运算 : 选择前三个图形, 运用公式: 第一图+第三图 =2*第二图 , 可得:2月亮+1圆= 2 圆,通过运算,可得 1圆= 2 月亮;② 替换 : 按照运算关系 ,将所有圆替换成月亮,可得月亮的数量规律为:1 2345 ,因此,选项处替换后应该为 6 个月亮。A替换后为8个月亮, D 替换后为4个月亮,C替换后为6个月亮。
因此,选择 C 选项。
思维2 : 该类题目也可以通过观察快速得到元素之间的运算关系,观察第二三四图,每个图形均有一个圆,但月亮的数量却在按0 12 的等差数列递增,如果按此猜想,第五图应该保持1个圆不变的同时,月亮数列为3,说明其中两个月亮 被 圆代替,得到1圆= 2 月亮,再代入题干进行替换,进一步得到规律。 省去了写运算公式的步骤,可以节省一定的时间。
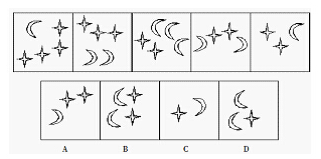
【例 2】 从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
【华图解析】 D
第一步,观察特征。
组成元素不同,优先考虑数量类或属性类。图形均由小元素组成,考虑数量类的元素。
第二步,两段式,第一段找规律,第二段应用规律。
思维1: 首先观察元素的种类或者个数,发现没有规律,再观察元素之间的加减乘除关系,仍然无规律。因此,考虑元素的运换算:① 运算 : 选择前三个图形,运用公式:第一图+第三图 =2*第二图, 可得: 6四角星+ 4 月亮= 6 四角星+ 4 月亮,发现该式子为恒等式,恒等式恰恰可以说明满足等差数列的特 征,刚好满足 第一图+第三图 =2*第二图 ,但是无法计算出四角星与月亮之间的数量关系,因此选择第二、三、四图进行运算,可得 :5四角星+ 4 月亮= 6 月亮+ 4 四角星,得 :1四角星= 2 月亮; ② 替换 :按照运算关系,将所有 四角星 替换成月亮,可得月亮的数量规律为: 9 8765 , 因此,选项处替换后应该为 4个月亮,A替换后为5个,B替换后为6,C替换后为3 ,D 替换后为4。
因此,选择 D 选项。
思维2 : 思维同 【例1】 , 观察 倒数三个图形,从后往前观察,发现 每个图形均有 2个四角星 ,但月亮的数量却在按 123 的等差数列递增,如果按此猜想,图 二 应该保持 2 个四角星 不变的同时,月亮数列为 4 ,说明其中 2 个月亮 被 1个四角星 代替,得到1 四角星 = 2 月亮,再代入题干进行替换,进一步得到规律。省去了写运算公式的步骤,可以节省一定的时间。
拓展: 等差数列还满足 公式: 第一图+第二图=第三图 ,例如1 23 , 246 等,因此有些题目可能设置运用此运算公式来确定元素之间的替换关系。











