1.存在一个这样的四位数,其十位数字等于个位数字加2,百位数字等于十位数字加1,现在如果把这个四位数字的各位数字依次颠倒,得到的新数跟原数之和等于11220,请问这个四位数除以3的余数是多少?
A.0 B.1
C.2 D.不确定
【答案】A
【解析】多位数问题
设这个四位数的个位数为X,则十位数字表示为X+2,百位表示为X+3,千位数设为Y,则这个数字为Y.X+3.X+2.X,颠倒之后为X.X+2.X+3.Y,得到结论,X+Y=10,X+2+X+3=11,联立两式解得X=3,Y=7,故这个四位数为7653,7653除以3的余数为0。
因此,选择A选项。



3.顺应贵阳市的“创文”活动的号召,小明、小王、小张自发组织去敬老院看望孤寡老人,由于三人的课余时间不一样,所以他们之间达成了以下约定,小明每3天去一次,小王每隔4天去一次,小张一个星期去一次,上次三人同时去养老院的时间是星期三,那么从这次开始三人第4次一同去养老院是星期几?
A.星期一 B.星期二
C.星期三 D.星期天
【答案】C
【解析】循环周期问题
小明3天去一次,小王相当于是4+1=5天去一次,小张是7天去一次,3,5,7的最小公倍数是105,相当于三人下一次再相遇是过了105天,105/7余数是0,所以下一次相遇的时间还是星期三,不管第几次相遇时间都是星期三,故第四次相遇的时间也是星期三。
因此,选择选项C。
4.贵阳观山大道某路段道路两旁各安装了21盏路灯,路灯与路灯之间的间距是一样的,现在市政部门响应市民的号召,为提高照明的亮度,决定在道路的两侧共加装12盏路灯,保证加装路灯之后相邻路灯之间的间距也保持相同,那么最多有几盏路灯不需要移动?
A.3 B.4
C.5 D.6
【答案】A
【解析】约倍数问题
原先道路一边安装了21盏路灯,所以道路的总长可以表示21-1=20的倍数,记作20N,N表示的是路灯之间的间隔长度,后面共增加12盏路灯,每边增加6盏,可知现在每边路灯为21+6=27盏,总长可以表示为27-1=26的倍数,记作26M,M为现在路灯之间的间距,实际上道路的总长可以设为20和26的最小公倍数260,故N=13,M=10,则不需要移动的路灯为13*10=130的公倍数,数下来有距起点0、130、260这3盏路灯是不需要移动的。
因此,选择A选项。
5.小明打算进行自主创业的尝试。他购买某种商品的进价是每件20元,以30元每件的价格进行出售,第一天就卖出了60件。为了提高销量,小明打算降价促销,第二天他发现每降价一元,销量就会提高10件,为保证获得最大利润,小明的定价应定成多少?(函数问题)
A.21 B.25
C.26 D.28
【答案】D
【解析】函数问题

这是经济利润问题中的函数应用问题。设小明获得的利润为Y,小明刚开始每件商品的利润为10元,销量为60,假设降价X元,利润Y=(10-X)(60+10*X),这是一个开口向下的二次函数,有最大值,最大值为10+(-6)=4的中点,故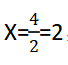 ,当X取得2的时候利润Y取得最大值,故定价定为30-2=28可获得最大利润。
,当X取得2的时候利润Y取得最大值,故定价定为30-2=28可获得最大利润。
因此,选择D选项。










